Dãy số không giải pháp đều là một trong loại bài xích toán rất gần gũi trong toán học, đặc biệt là trong những bài tập tính tổng. Không giống với dãy số có khoảng cách đều giữa các số hạng, hàng số ko cách đều sở hữu sự thay đổi không đồng số đông về giá trị giữa những số hạng trong dãy. Việc tính tổng của rất nhiều dãy số này yên cầu sự phát âm biết thâm thúy về các quy luật cấu trúc dãy số với cách áp dụng các cách thức tính tổng phù hợp. Trong bài viết này, chúng ta sẽ kiếm tìm hiểu phương thức tính tổng hàng số không phương pháp đều qua các ví dụ và bài tập minh họa, giúp người đọc nắm rõ kiến thức và kỹ năng giải quyết và xử lý loại câu hỏi này.

Bạn đang xem: Bài tập tính tổng dãy số không cách đều

Giới Thiệu Về dãy Số Không bí quyết Đều

Dãy số không phương pháp đều là hầu như dãy số mà các số hạng không có khoảng cách đều nhau. Điều này có nghĩa là sự chênh lệch giữa các số hạng liên tiếp trong dãy chưa phải lúc nào cũng giống nhau. Một ví dụ thông dụng của hàng số không phương pháp đều là hàng số Fibonacci, trong đó mỗi số hạng là tổng của hai số hạng trước đó. Không giống với dãy số số học tập (có khoảng cách đều giữa các số hạng), dãy số không phương pháp đều hoàn toàn có thể tạo ra nhiều kiểu tăng trưởng không giống nhau, và vị vậy phương pháp tính tổng của bọn chúng cũng yên cầu các phương thức khác biệt.

Định Nghĩa hàng Số Không phương pháp Đều

Dãy số không giải pháp đều là một trong dãy số mà không có một khoảng chừng cách cố định và thắt chặt giữa những số hạng liên tiếp. Chẳng hạn, hàng số Fibonacci có những số hạng sau: 1, 1, 2, 3, 5, 8, 13, 21, … Sự vững mạnh của dãy số này không phải là một trong những số thắt chặt và cố định mà chuyển đổi dần theo từng bước.

Phân Biệt dãy Số phương pháp Đều với Không bí quyết Đều

Trong dãy số phương pháp đều, sự khác hoàn toàn giữa những số hạng tiếp tục là một hằng số. Ví dụ, trong dãy số số học tập 2, 4, 6, 8, 10, …, sự khác hoàn toàn giữa các số hạng là 2. Ngược lại, trong hàng số không bí quyết đều, sự khác hoàn toàn này biến hóa và không theo quy giải pháp cố định, ví như dãy số Fibonacci hoặc những dãy số đặc trưng khác.

Phương Pháp Tính Tổng dãy Số Không biện pháp Đều

Việc tính tổng dãy số không biện pháp đều phụ thuộc vào vào việc nắm rõ quy phương tiện của hàng số. Các cách thức thông dụng bao hàm việc dìm diện quy cách thức số học, sử dụng công thức tổng quát hoặc áp dụng các thuật toán tìm kiếm và thống kê giám sát tổng hiệu quả.

Xác Định Quy chính sách Của dãy Số

Trước lúc tính tổng của một hàng số không biện pháp đều, việc đầu tiên cần làm là xác định quy chế độ của dãy số. Điều này rất có thể yêu cầu một số trong những kiến thức về các loại dãy số như hàng số Fibonacci, dãy số hình học, hay dãy số tăng theo một hàm số sệt biệt. Sau thời điểm nhận diện được quy luật pháp này, chúng ta có thể sử dụng các công thức hoặc cách thức phù hợp để tính tổng.

Phương Pháp Tính Tổng dãy Số Không phương pháp Đều

Để tính tổng hàng số không phương pháp đều, bạn cũng có thể áp dụng các cách thức như sau:

• Phương pháp cộng dồn: Đơn giản duy nhất là cộng dồn từng số hạng trong dãy. Phương thức này rất có thể áp dụng cho những dãy số ngắn hoặc không thực sự phức tạp.
• Sử dụng bí quyết tổng quát: một số dãy số tất cả công thức tổng quát (ví dụ, dãy số Fibonacci tất cả công thức F(n) = F(n-1) + F(n-2)). Áp dụng cách làm này sẽ giúp đỡ tính tổng cấp tốc chóng.
• Áp dụng thuật toán: Đối với các dãy số bao gồm quy cách thức phức tạp, bạn cũng có thể cần sử dụng những thuật toán đo lường tối ưu, ví dụ như thuật toán đệ quy hoặc sử dụng các công thức tổng quát cho những dãy số sệt biệt.

  Xem thêm: Hướng dẫn chi tiết cách lưu dữ liệu lên Google Drive

Ví Dụ Minh Họa

Để làm rõ hơn về phong thái tính tổng hàng số không giải pháp đều, hãy thuộc xem qua một số trong những ví dụ minh họa bên dưới đây:

Ví Dụ 1: Tính Tổng dãy Số Fibonacci

Dãy số Fibonacci là 1 trong dãy số quan trọng đặc biệt trong kia mỗi số hạng là tổng của nhị số hạng trước đó. Hàng số Fibonacci bước đầu với 1 cùng 1, tiếp đến tiếp theo là các số: 2, 3, 5, 8, 13, 21, 34, …

Công thức tính tổng của hàng số Fibonacci tự F(1) mang đến F(n) là:

Tổng = F(1) + F(2) + ... + F(n)

Ví dụ, nếu như n = 5, tổng của hàng số Fibonacci là: 1 + 1 + 2 + 3 + 5 = 12.

Ví Dụ 2: Tính Tổng hàng Số Hình Thang

Dãy số hình thang là dãy số bao gồm sự vững mạnh không đều giữa những số hạng. Ví dụ, một hàng số có những số hạng sau: 1, 4, 9, 16, 25, …

Công thức tính tổng của hàng số hình thang có thể sử dụng cách thức cộng dồn những số hạng hoặc áp dụng công thức tổng quát cho các dãy số hình học.

Bài Tập Vận Dụng

Để củng cầm cố kỹ năng, dưới đó là một số bài tập vận dụng về tính tổng hàng số không giải pháp đều.

Bài Tập 1: Tính Tổng hàng Số 1, 2, 3, 5, 8, 13, …

Dãy số bên trên là một phần của hàng số Fibonacci. Cùng dồn các số hạng này: 1 + 2 + 3 + 5 + 8 + 13 = 32.

Bài Tập 2: Tính Tổng dãy Số 1, 4, 9, 16, 25, …

Đây là 1 dãy số hình thang. Cùng dồn những số hạng: 1 + 4 + 9 + 16 + 25 = 55.

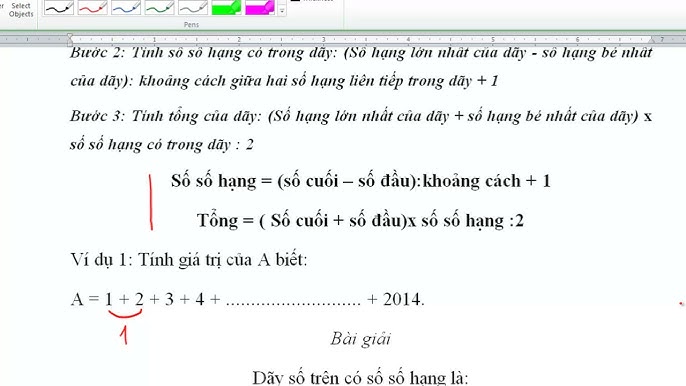
Lưu Ý Khi giải quyết Bài thói quen Tổng dãy Số Không bí quyết Đều

Khi giải quyết các bài xích tập tính tổng hàng số không bí quyết đều, chúng ta cần chú ý một số điểm quan tiền trọng:

Kiểm Tra Quy qui định Của dãy Số

Việc dấn diện đúng quy qui định của dãy số là khôn cùng quan trọng. Một số trong những dãy số gồm công thức tổng quát, trong khi một số khác yêu cầu bạn tìm hiểu thêm về những số hạng trước đó để tính toán. Đảm bảo bạn đã đọc rõ cách thức tính toán trước lúc bắt đầu.

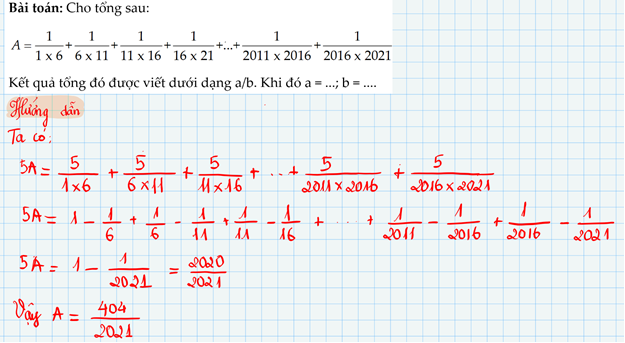
Áp Dụng phương pháp Tính Tổng Phù Hợp

Tùy trực thuộc vào dãy số, bạn cũng có thể áp dụng cách thức cộng dồn, công thức tổng quát, hoặc thuật toán về tối ưu. Việc chọn phương thức đúng sẽ giúp bạn tính tổng một cách hối hả và chủ yếu xác.

Tổng Kết

Tính tổng hàng số không biện pháp đều là một trong những kỹ năng quan trọng đặc biệt trong toán học. Việc làm rõ quy pháp luật của dãy số với áp dụng phương pháp tính tổng phù hợp sẽ góp bạn xử lý các vấn đề này tác dụng hơn. Hãy luyện tập liên tiếp và áp dụng những cách thức đã học để nâng cao kỹ năng của mình trong vấn đề tính tổng hàng số không bí quyết đều.