Không gian Euclid là một trong khái niệm quan trọng trong toán học, nhất là trong các lĩnh vực hình học, đại số đường tính và lý thuyết vector. Với những bài tập không khí Euclid, học viên và sinh viên rất có thể hiểu sâu hơn về các khái niệm cơ bạn dạng và áp dụng trong toán học. Bài viết này đang đi sâu vào những bài tập không gian Euclid, cung ứng lời giải chi tiết cho từng bài, đồng thời phân tích và lý giải các phương pháp và chuyên môn giải toán hiệu quả.

Bạn đang xem: Bài tập không gian euclide có lời giải

Giới Thiệu Về không gian Euclid

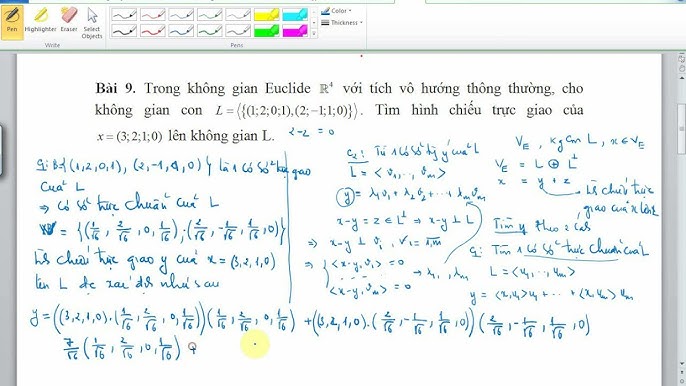
Định Nghĩa và có mang Cơ Bản

Không gian Euclid, theo tên của nhà toán học tập Euclid, là một không khí trong đó các điểm, đường thẳng và những hình học được xác minh thông qua những hệ tọa độ. Không gian Euclid 2d (hai chiều) và 3d (ba chiều) là hồ hết khái niệm phổ biến mà họ gặp yêu cầu trong toán học cùng khoa học. Các giám sát liên quan mang đến vectơ, khoảng cách, góc và tích vô hướng phần lớn dựa trên những quy tắc của không khí Euclid.

Lịch Sử cách tân và phát triển và Ứng Dụng

Không gian Euclid đã xuất hiện từ thời cổ kính và là nền tảng của rất nhiều lý thuyết hình học hiện nay đại. Euclid, trong thành công "Elements" (Các yếu tố), vẫn mô tả những định lý và chứng minh các đặc điểm của hình học trong không gian hai chiều. Các nguyên tắc của Euclid vẫn tồn tại qua nhiều thế kỷ và trở nên cơ sở đến các nghiên cứu về hình học cùng đại số tuyến đường tính ngày nay. Ứng dụng của không gian Euclid hiện diện trong các nghành nghề như công nghệ máy tính, kỹ thuật, đồ vật lý và cả trong các môn học như đồ họa máy tính, robot học, và thậm chí trong y học.

Các Dạng bài Tập Thường chạm chán Trong không gian Euclid

Tính Tích Vô Hướng

Tích vô hướng (hay có cách gọi khác là tích scala) của hai vectơ là một trong những phép toán đặc biệt quan trọng trong không khí Euclid. Tích vô hướng thân hai vectơ A với B được tính theo công thức:

A . B = |A| * |B| * cos(θ), trong đó θ là góc thân hai vectơ A và B, |A| cùng |B| theo lần lượt là độ dài của những vectơ A với B.

Ví dụ: giả dụ A = (3, 4) với B = (1, 2), thì tích vô hướng của A cùng B được xem như sau: A . B = (3 * 1) + (4 * 2) = 11.

Tính Độ dài Vectơ

Để tính độ dài của một vectơ trong không gian Euclid, ta sử dụng công thức Pythagore trong không gian hai chiều hoặc bố chiều. Độ lâu năm của vectơ A = (x1, y1) trong không gian hai chiều được xem bằng:

|A| = √(x1² + y1²).

Ví dụ: Đối cùng với vectơ A = (3, 4), độ nhiều năm của A là √(3² + 4²) = √25 = 5.

Góc thân Hai Vectơ

Góc thân hai vectơ A và B trong không khí Euclid được xem theo công thức:

cos(θ) = (A . B) / (|A| * |B|), trong đó A . B là tích vô hướng của hai vectơ A và B, cùng |A|, |B| là độ nhiều năm của chúng.

Ví dụ, với A = (1, 0) và B = (0, 1), ta tất cả A . B = 0, cho nên cos(θ) = 0, từ kia suy ra θ = 90 độ.

Phép Chiếu Vectơ

Phép chiếu của một vectơ A lên một vectơ khác B trong không khí Euclid được xem bằng công thức:

proj(B)A = ((A . B) / (B . B)) * B.

Phép chiếu giúp ta làm rõ hơn về mối quan hệ giữa các vectơ và thường được sử dụng trong số bài tập về không gian vector và hình học phân tích.

Phép đổi mới Hình Trong không khí Euclid

Trong không khí Euclid, các phép biến ngoài ra dịch chuyển, quay, bức xạ giúp thay đổi vị trí của những điểm mà lại không làm biến hóa hình dạng và size của chúng. Phần nhiều phép trở thành hình này rất đặc biệt quan trọng trong những bài tập và định hướng toán học, đặc biệt quan trọng trong hình học tập và kim chỉ nan nhóm.

Ví dụ, phép con quay của một điểm P(x, y) quanh gốc tọa độ (0, 0) một góc θ sẽ sở hữu được công thức:

x’ = x * cos(θ) - y * sin(θ), y’ = x * sin(θ) + y * cos(θ).

Hướng Dẫn Giải cụ thể Các bài xích Tập Mẫu

Bài Tập 1: Tính Tích Vô Hướng

Giải bài xích tập tính tích vô hướng giữa hai vectơ A = (2, 3) với B = (4, 1):

Bước 1: Áp dụng cách làm tích vô hướng: A . B = (2 * 4) + (3 * 1) = 8 + 3 = 11.

Bước 2: kết quả tích vô hướng giữa A với B là 11.

Bài Tập 2: Tính Độ dài Vectơ

Cho vectơ A = (5, 12), tính độ nhiều năm của A:

Bước 1: Áp dụng công thức độ lâu năm vectơ: |A| = √(5² + 12²) = √169 = 13.

Bước 2: Độ lâu năm của A là 13.

Xem thêm: Hội đồng tái thẩm không có quyền sửa bản án, Phân tích và giải đáp

Bài Tập 3: Xác Định Góc giữa Hai Vectơ

Cho hai vectơ A = (1, 1) và B = (2, 2), xác định góc giữa chúng:

Bước 1: Tính tích vô phía A . B: A . B = (1 * 2) + (1 * 2) = 4.

Bước 2: Tính độ dài của A và B: |A| = √(1² + 1²) = √2, |B| = √(2² + 2²) = √8.

Bước 3: Tính cos(θ): cos(θ) = 4 / (√2 * √8) = 1, từ đó suy ra θ = 0 độ.

Bài Tập 4: Phép Chiếu Vectơ

Cho vectơ A = (3, 4) và B = (1, 0), tính phép chiếu của A lên B:

Bước 1: Tính tích vô phía A . B = (3 * 1) + (4 * 0) = 3.

Bước 2: Tính B . B = (1 * 1) + (0 * 0) = 1.

Bước 3: Phép chiếu của A lên B là: proj(B)A = (3 / 1) * (1, 0) = (3, 0).

Bài Tập 5: Phép biến hóa Hình Trong không khí Euclid

Cho điểm P(1, 2), thực hiện phép quay điểm p quanh nơi bắt đầu tọa độ 90 độ. Tính tọa độ new của P:

Bước 1: Áp dụng công thức quay: x’ = 1 * cos(90) - 2 * sin(90) = 0 - 2 = -2, y’ = 1 * sin(90) + 2 * cos(90) = 1 + 0 = 1.

Bước 2: Tọa độ new của p. Là (-2, 1).

Các lưu lại Ý lúc Giải bài xích Tập không gian Euclid

Phương Pháp Tiếp Cận Hiệu Quả

Để giải các bài tập về không gian Euclid hiệu quả, cần để ý đến bài toán nắm vững những công thức cơ phiên bản và cách áp dụng chúng trong từng trường hợp cụ thể. Học viên cần đề xuất luyện tập liên tục để hiểu rõ các quan niệm và các bước giải bài bác toán.

Tránh những Lỗi thường Gặp

Một số lỗi thường chạm mặt khi giải bài xích tập không gian Euclid bao hàm việc quên áp dụng công thức đúng hoặc tính không nên độ dài của các vectơ. Học viên cũng rất có thể nhầm lẫn trong việc xác minh các góc giữa các vectơ, bởi vì vậy cần thực hành thực tế thật các để tránh sai sót.

Tài Liệu xem thêm và Nguồn học Tập

Sách Giáo Khoa cùng Tài Liệu Tham Khảo

Các sách giáo khoa về đại số tuyến tính và hình học tập là mối cung cấp tài liệu quan trọng đặc biệt để học sinh và sinh viên tìm hiểu về không khí Euclid. Phần lớn cuốn sách này thường hỗ trợ đầy đủ lý thuyết và bài bác tập kèm lời giải chi tiết, giúp bạn học cụ vững những khái niệm và phương thức giải toán.

Các trang web và Diễn Đàn học tập Tập

Các trang web học tập như Khan Academy, Coursera, hoặc những diễn bọn học toán trực tuyến đường là những nơi lý tưởng nhằm tìm kiếm thêm tài liệu với tham gia luận bàn với các bạn học khác. Hầu như nguồn này không chỉ giúp bạn củng cố định hướng mà còn cung cấp bài tập thực hành thực tế phong phú.

Câu Hỏi Thường chạm mặt (FAQ)

Không Gian Euclid tất cả Ứng Dụng Gì trong Thực Tiễn?

Không gian Euclid có nhiều ứng dụng thực tiễn, quan trọng trong các nghành nghề như kỹ thuật, thiết bị lý và hình ảnh máy tính. Trong thứ lý, không gian Euclid góp mô tả hoạt động của những vật thể, còn vào kỹ thuật, nó cung cấp việc thống kê giám sát các lực ảnh hưởng lên những vật thể trong không gian ba chiều.

Làm gắng Nào Để cải thiện Kỹ Năng Giải bài Tập không gian Euclid?

Để nâng cao kỹ năng giải bài xích tập không khí Euclid, bạn phải thực hành liên tục và học hỏi và chia sẻ từ những bài bác tập mẫu. Lân cận đó, tham gia các lớp học tập trực con đường hoặc nhóm học tập có thể giúp bạn làm rõ hơn về các phương thức giải toán.

Kết Luận

Tóm Tắt câu chữ Chính

Thông qua bài viết này, các bạn đã được ra mắt về không gian Euclid và các bài tập liên quan. Các bài tập không gian Euclid giúp người học hiểu rõ hơn về các khái niệm như tích vô hướng, độ lâu năm vectơ, góc giữa các vectơ và các phép đổi thay hình.

Khuyến Khích Đọc Thêm và Thực Hành

Để thành thạo không khí Euclid, bạn phải thực hành tiếp tục và đọc thêm từ những tài liệu học tập phong phú. Vấn đề rèn luyện qua những bài tập để giúp bạn vậy vững lý thuyết và năng lực giải toán nhanh chóng.