Khoảng phương pháp trong không khí là một khái niệm đặc biệt trong hình học không gian, có ứng dụng rộng rãi trong các nghành nghề từ toán học, đồ vật lý đến phong cách xây dựng và kỹ thuật. Nội dung bài viết này đã cung cấp cho bạn những loài kiến thức cần thiết để giải quyết và xử lý các bài bác tập tương quan đến khoảng cách trong ko gian, bao gồm các cách thức giải cụ thể cho từng dạng bài tập phổ biến, cũng tương tự ứng dụng thực tế của chúng.

Bạn đang xem: Bài tập khoảng cách trong không gian

Khoảng bí quyết Trong không gian Là Gì?

Khi nói tới hình học tập không gian, khoảng cách là một đại lượng đo độ lâu năm giữa các đối tượng người dùng trong không gian ba chiều. Đây là một trong những yếu tố cơ bạn dạng giúp bọn họ tính toán với phân tích những vị trí của những điểm, mặt đường thẳng với mặt phẳng trong không gian. Việc tính toán khoảng bí quyết này có thể được vận dụng vào những tình huống thực tế như trong thi công kiến trúc, bối cảnh 3D, hay nghiên cứu khoa học.

Các Dạng bài bác Tập phổ cập Về khoảng cách Trong không Gian

Có các loại bài bác tập về khoảng cách trong không gian mà bạn cũng có thể gặp phải. Dưới đấy là các dạng bài tập phổ biến, bao gồm cách khẳng định khoảng giải pháp giữa các đối tượng người sử dụng trong ko gian:

Khoảng biện pháp Từ Điểm Đến Đường Thẳng

Để tính khoảng cách từ một điểm đến một con đường thẳng trong ko gian, bọn họ cần sử dụng công thức dựa vào vector pháp con đường của mặt đường thẳng và vị trí của điểm trong ko gian. Khoảng cách này là chiều nhiều năm của đoạn vuông góc từ điểm đến đường thẳng.

Khoảng bí quyết Từ Điểm Đến phương diện Phẳng

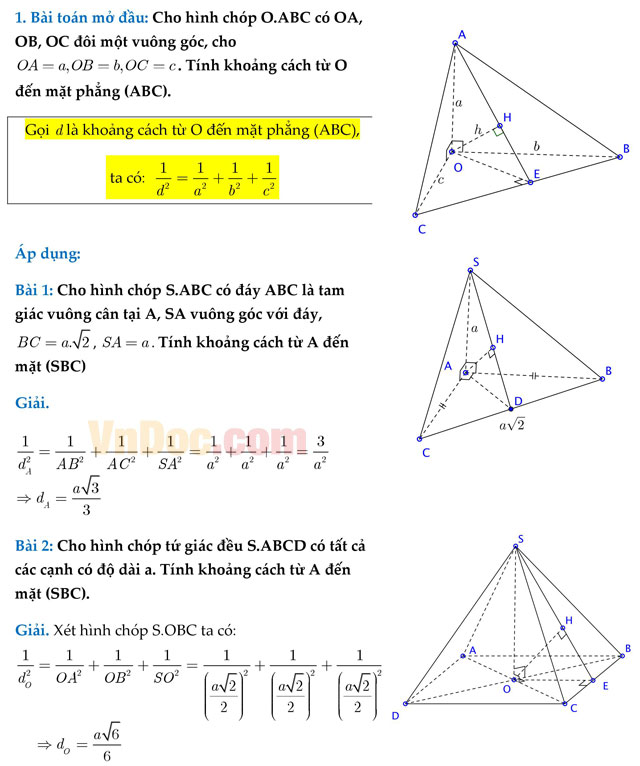
Khoảng bí quyết từ một điểm đến mặt phẳng trong ko gian hoàn toàn có thể tính bởi công thức thực hiện tích vô hướng thân vector pháp tuyến đường của phương diện phẳng với vector nối từ điểm đến mặt phẳng. Đây là một trong những bài toán cơ phiên bản trong hình học không gian.

Khoảng giải pháp Giữa hai Đường Thẳng chéo cánh Nhau

Khi hai đường thẳng không tuy vậy song với không giảm nhau, bọn họ sẽ tính khoảng cách giữa chúng thông qua việc tìm kiếm đoạn vuông góc thông thường của hai tuyến phố thẳng. Cách thức này thường yêu cầu kiến thức về vector và các phép toán đại số tuyến tính.

Khoảng phương pháp Giữa hai Mặt Phẳng song Song

Khoảng bí quyết giữa nhì mặt phẳng song song được xác định bằng cách tính khoảng cách từ một điểm thuộc mặt phẳng này cho mặt phẳng kia. Việc vận dụng công thức về khoảng cách từ điểm đến chọn lựa mặt phẳng sẽ giúp bạn tra cứu được hiệu quả chính xác.

Khoảng biện pháp Giữa Đường Thẳng cùng Mặt Phẳng tuy nhiên Song

Trong ngôi trường hợp con đường thẳng và mặt phẳng tuy vậy song, khoảng cách giữa chúng sẽ tiến hành tính bằng cách lấy khoảng cách từ điểm thuộc đường thẳng cho mặt phẳng. Phương thức này tựa như như tính khoảng cách từ điểm đến lựa chọn mặt phẳng trải qua công thức áp dụng vector pháp tuyến.

Phương Pháp Giải những Dạng bài Tập Về khoảng cách Trong không Gian

Phương Pháp Giải khoảng cách Từ Điểm Đến Đường Thẳng

Để giải bài bác tập về khoảng cách từ điểm đến đường thẳng, bạn cần xác định vector pháp tuyến đường của mặt đường thẳng cùng vector nối từ điểm đến chọn lựa đường trực tiếp đó. Sau đó, thực hiện công thức:

Khoảng biện pháp = |(P-Q) . N| / |n|

Trong đó:

• P là vấn đề cần tính khoảng tầm cách.
• Q là điểm ngẫu nhiên trên đường thẳng.
• n là vector pháp tuyến đường của con đường thẳng.

Phương Pháp Giải khoảng cách Từ Điểm Đến khía cạnh Phẳng

Để tính khoảng cách từ điểm đến lựa chọn mặt phẳng, công thức thực hiện như sau:

Khoảng bí quyết = |(P-Q) . N| / |n|

Trong đó:

• P là vấn đề cần tính khoảng tầm cách.
• Q là 1 điểm thuộc mặt phẳng.
• n là vector pháp tuyến đường của phương diện phẳng.

Phương Pháp Giải khoảng cách Giữa nhì Đường Thẳng chéo Nhau

Đối với bài bác toán khoảng cách giữa hai tuyến đường thẳng chéo cánh nhau, bạn cần tìm đoạn vuông góc bình thường giữa chúng và tính độ lâu năm của đoạn này bằng cách sử dụng công thức:

Khoảng bí quyết = |(A1 - A2) . (B1 x B2)| / |B1 x B2|

Trong kia A1, A2 là các điểm thuộc hai tuyến đường thẳng cùng B1, B2 là những vector chỉ phương của hai tuyến đường thẳng.

Phương Pháp Giải khoảng cách Giữa nhị Mặt Phẳng tuy vậy Song

Khi tính khoảng cách giữa nhì mặt phẳng tuy nhiên song, chúng ta cần xác minh khoảng cách xuất phát từ một điểm ở trong một phương diện phẳng đến mặt phẳng còn lại. Bí quyết được sử dụng là:

Khoảng phương pháp = |(P-Q) . N| / |n|

Phương Pháp Giải khoảng cách Giữa Đường Thẳng với Mặt Phẳng song Song

Để giải việc này, bạn cần tính khoảng cách từ một điểm thuộc con đường thẳng cho mặt phẳng tuy vậy song. Cách thức này thực hiện công thức tính khoảng cách từ điểm đến lựa chọn mặt phẳng cùng với vector pháp con đường của phương diện phẳng.

Bài Tập thực hành thực tế Có lời giải Chi Tiết

Bài Tập 1: Tính khoảng cách Từ Điểm Đến Đường Thẳng

Cho điểm P(2,3,4) và đường thẳng d có phương trình r = (1,2,3) + t(2, -1, 1). Tính khoảng cách từ điểm p. đến đường thẳng d.

Xem thêm: Những Đề Giải Bài Toán Bằng Cách Lập Phương Trình - Hướng Dẫn Chi Tiết và Bài Tập Thực Hành

Lời giải: Đầu tiên, ta tính vector PQ từ bỏ điểm phường đến một điểm Q trên tuyến đường thẳng d, tiếp đến áp dụng phương pháp đã học nhằm tính khoảng tầm cách.

Bài Tập 2: Tính khoảng cách Từ Điểm Đến phương diện Phẳng

Cho điểm P(3, 4, 5) và mặt phẳng có phương trình 2x - 3y + z = 6. Tính khoảng cách từ điểm p đến khía cạnh phẳng này.

Lời giải: Ta sử dụng công thức khoảng cách từ điểm đến chọn lựa mặt phẳng, chũm giá trị của điểm p vào và tính kết quả.

Bài Tập 3: Tính khoảng cách Giữa nhị Đường Thẳng chéo Nhau

Cho hai tuyến phố thẳng d1: r = (1, 2, 3) + t(2, -1, 1) cùng d2: r = (4, 5, 6) + s(1, 1, -1). Tính khoảng cách giữa hai đường thẳng này.

Lời giải: sử dụng công thức khoảng cách giữa hai đường thẳng chéo nhau nhằm tìm kết quả.

Bài Tập 4: Tính khoảng cách Giữa hai Mặt Phẳng tuy nhiên Song

Cho nhị mặt phẳng x + 2y + 3z = 4 cùng x + 2y + 3z = 7. Tính khoảng cách giữa chúng.

Lời giải: Áp dụng bí quyết tính khoảng cách giữa hai mặt phẳng tuy vậy song.

Bài Tập 5: Tính khoảng cách Giữa Đường Thẳng với Mặt Phẳng tuy vậy Song

Cho đường thẳng r = (1, 2, 3) + t(2, -1, 1) với mặt phẳng x + 2y + 3z = 6. Tính khoảng cách giữa đường thẳng với mặt phẳng này.

Lời giải: Áp dụng công thức khoảng cách từ điểm đến chọn lựa mặt phẳng và điều chỉnh cho thích hợp với tình huống.

Ứng Dụng Của việc Tính khoảng cách Trong Thực Tế

Việc tính khoảng cách trong không gian có ứng dụng rất to lớn trong các lĩnh vực, từ xây cất kiến trúc, thiết bị lý, đến công nghệ máy tính và bối cảnh 3D. Dưới đó là một số ứng dụng thực tiễn của vấn đề tính khoảng cách trong ko gian:

Ứng Dụng Trong bản vẽ xây dựng và Xây Dựng

Trong con kiến trúc, đo lường và thống kê khoảng cách giữa các đối tượng người tiêu dùng giúp xác xác định trí và kích cỡ của những công trình xây dựng. Điều này rất đặc biệt quan trọng khi thiết kế các dự án công trình lớn như cầu, tòa nhà và các công trình tinh vi khác.

Ứng Dụng Trong đồ dùng Lý và Kỹ Thuật

Trong đồ dùng lý, khoảng cách giữa các đối tượng người sử dụng trong không khí có thể tác động đến các đo lường và tính toán về lực hấp dẫn, tự trường, và các hiện tượng trang bị lý khác. Những kỹ sư cũng sử dụng các công thức tính khoảng cách này vào việc xây dựng các khối hệ thống cơ học cùng điện tử.

Ứng Dụng trong Khoa Học máy tính và Đồ Họa 3D

Trong technology đồ họa 3 chiều và các ứng dụng khoa học máy tính, việc tính toán khoảng giải pháp giữa các đối tượng người dùng giúp tạo nên các mô hình 3D bao gồm xác, về tối ưu hóa hiệu suất và nâng cao chất lượng hình hình ảnh trong những trò chơi điện tử hoặc các ứng dụng mô phỏng.

Lưu Ý lúc Giải các Bài Tập Về khoảng tầm Cách

Khi giải các bài tập về khoảng cách trong không gian, các bạn cần để ý một số điểm sau:

• Kiểm tra độ đúng đắn của dữ liệu đầu vào trước khi tính toán.
• Chọn phương pháp giải phù hợp với từng dạng bài bác tập.
• Thực hành tiếp tục để nâng cấp kỹ năng và nâng cao khả năng xử lý các bài bác toán tinh vi hơn.

Để thực hành thực tế và cải thiện kỹ năng tính toán khoảng phương pháp trong ko gian, chúng ta cũng có thể tham khảo các tài liệu với sách giáo khoa gồm sẵn trên thị phần hoặc tra cứu kiếm các khóa học tập trực tuyến. Sự thực hành là yếu hèn tố quan trọng giúp chúng ta hiểu cùng áp dụng kim chỉ nan vào thực tiễn một bí quyết hiệu quả.